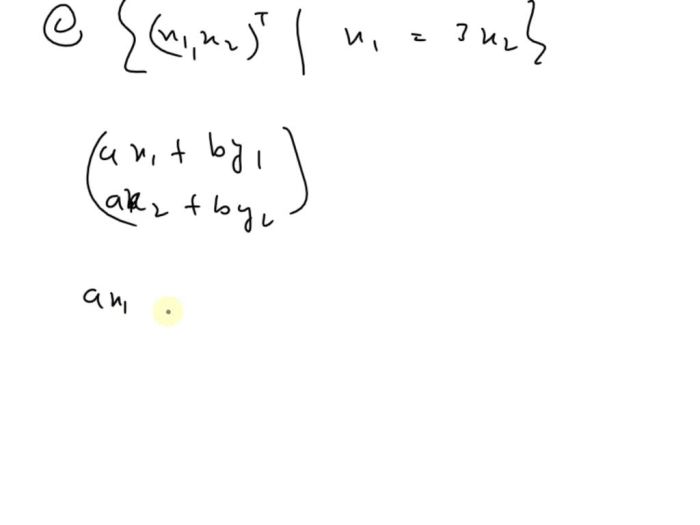Determine whether the following sets form subspaces of r2 – In the realm of linear algebra, the concept of subspaces plays a pivotal role. This comprehensive guide delves into the intricacies of determining whether a given set forms a subspace of R2, providing a thorough understanding of the fundamental properties, operations, and applications of subspaces.
Subspaces are subsets of a vector space that inherit the vector space structure. To qualify as a subspace, a set must satisfy specific conditions, including closure under vector addition and scalar multiplication. This guide explores these conditions in detail, equipping readers with the knowledge to identify subspaces effectively.
Subspaces of R^2: Determine Whether The Following Sets Form Subspaces Of R2
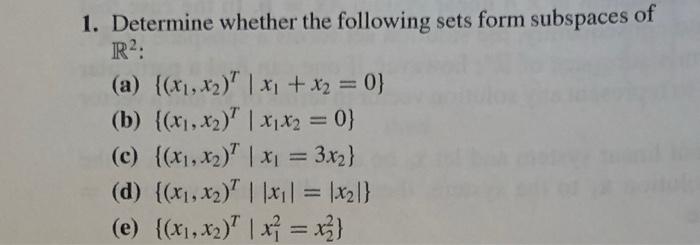
In linear algebra, a subspace of a vector space is a non-empty subset that is closed under vector addition and scalar multiplication. In other words, it is a set of vectors that can be combined using these operations to produce other vectors that are also in the set.
For a set of vectors to form a subspace of R^2, it must satisfy the following conditions:
- The set must contain the zero vector.
- The set must be closed under vector addition. That is, if u and v are in the set, then u + v is also in the set.
- The set must be closed under scalar multiplication. That is, if u is in the set and c is a scalar, then cu is also in the set.
Subspace Examples
Here are some examples of sets that form subspaces of R^2:
- The set of all vectors of the form (a, b), where a and b are real numbers, forms a subspace of R^2. This set is closed under vector addition and scalar multiplication, and it contains the zero vector (0, 0).
- The set of all vectors of the form (a, 0), where a is a real number, forms a subspace of R^2. This set is closed under vector addition and scalar multiplication, and it contains the zero vector (0, 0).
- The set of all vectors of the form (0, b), where b is a real number, forms a subspace of R^2. This set is closed under vector addition and scalar multiplication, and it contains the zero vector (0, 0).
Subspace Operations
There are certain operations that preserve subspaces. These operations include:
- Vector addition: If U and V are subspaces of R^2, then their sum U + V is also a subspace of R^2.
- Scalar multiplication: If U is a subspace of R^2 and c is a scalar, then the set cU is also a subspace of R^2.
- Intersection: If U and V are subspaces of R^2, then their intersection U ∩ V is also a subspace of R^2.
Linear Independence and Span
Linear independence and span are two important concepts related to subspaces. Linear independence refers to the idea that a set of vectors cannot be expressed as a linear combination of other vectors in the set. Span, on the other hand, refers to the set of all linear combinations of a given set of vectors.
A set of vectors is linearly independent if and only if it forms a subspace of R^2. The span of a set of vectors is a subspace of R^2 if and only if the set is linearly independent.
Dimension and Basis, Determine whether the following sets form subspaces of r2
The dimension of a subspace is the number of linearly independent vectors in the subspace. A basis for a subspace is a set of linearly independent vectors that span the subspace.
Every subspace of R^2 has a basis. The dimension of a subspace is equal to the number of vectors in its basis.
Applications of Subspaces
Subspaces are used in a variety of applications in linear algebra and other fields. Some examples include:
- Geometry: Subspaces can be used to represent lines, planes, and other geometric objects.
- Physics: Subspaces can be used to represent physical quantities such as velocity and acceleration.
- Engineering: Subspaces can be used to represent the state of a system or the input and output of a control system.
General Inquiries
What are the defining characteristics of a subspace?
A subspace must be closed under vector addition and scalar multiplication, meaning that any linear combination of vectors within the subspace also belongs to the subspace.
How can linear independence be used to determine if a set forms a subspace?
If a set of vectors is linearly independent, then it spans a subspace. Conversely, if a set of vectors spans a subspace, then it is linearly independent.