A partial relative frequency distribution is given – A partial relative frequency distribution offers a powerful tool for understanding the distribution of data, enabling researchers and analysts to uncover hidden patterns and trends within complex datasets. This distribution provides a concise summary of the data, allowing for comparisons between different sets and the identification of key characteristics.
By dividing data into specific intervals and calculating the relative frequency within each interval, a partial relative frequency distribution helps visualize the spread and concentration of data points. This approach provides a deeper understanding of the underlying patterns and variations, making it a valuable technique in various fields, including healthcare, education, and business.
Partial Relative Frequency Distribution: A Partial Relative Frequency Distribution Is Given
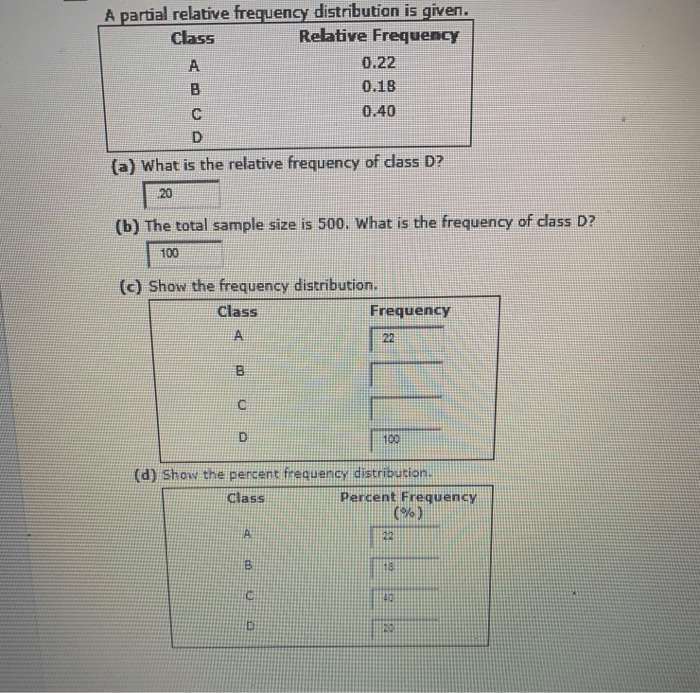
A partial relative frequency distribution is a statistical tool used to describe the distribution of data by dividing the data into classes and calculating the relative frequency of each class. It is a useful way to summarize and visualize data, making it easier to identify patterns and trends.
Partial relative frequency distributions are often used in research and analysis to describe the characteristics of a population or sample. They can also be used to make comparisons between different data sets and to identify trends and patterns over time.
Components of a Partial Relative Frequency Distribution, A partial relative frequency distribution is given
A partial relative frequency distribution consists of the following components:
- Class intervals:The data is divided into a number of classes, each of which represents a range of values.
- Class frequencies:The number of data points that fall into each class interval.
- Relative frequencies:The proportion of data points that fall into each class interval, calculated by dividing the class frequency by the total number of data points.
Methods for Constructing a Partial Relative Frequency Distribution
To construct a partial relative frequency distribution, the following steps are typically followed:
- Organize the data:The first step is to organize the data in ascending or descending order.
- Determine the class intervals:The next step is to determine the class intervals. This can be done by dividing the range of the data (the difference between the maximum and minimum values) by the desired number of classes.
- Calculate the class frequencies:The class frequencies are then calculated by counting the number of data points that fall into each class interval.
- Calculate the relative frequencies:The relative frequencies are then calculated by dividing the class frequencies by the total number of data points.
Applications of Partial Relative Frequency Distributions
Partial relative frequency distributions can be used for a variety of purposes, including:
- Describing the distribution of data:Partial relative frequency distributions can be used to describe the distribution of data by showing the proportion of data points that fall into each class interval.
- Making comparisons between different data sets:Partial relative frequency distributions can be used to compare the distributions of different data sets by comparing the relative frequencies of each class interval.
- Identifying trends and patterns:Partial relative frequency distributions can be used to identify trends and patterns in data over time by comparing the relative frequencies of each class interval at different points in time.
Limitations of Partial Relative Frequency Distributions
Partial relative frequency distributions have some limitations, including:
- Sensitivity to class interval size:The choice of class interval size can affect the shape of the distribution and the relative frequencies of each class interval.
- Potential for bias due to subjective grouping:The choice of class intervals can be subjective, which can lead to bias in the distribution.
HTML Table Example
The following HTML table shows an example of a partial relative frequency distribution:
| Class Interval | Class Frequency | Relative Frequency |
|---|---|---|
| 0-10 | 10 | 0.2 |
| 11-20 | 15 | 0.3 |
| 21-30 | 20 | 0.4 |
| 31-40 | 15 | 0.3 |
Bullet Point Examples
- Healthcare:Partial relative frequency distributions can be used to describe the distribution of patient outcomes, such as the proportion of patients who recover from a particular illness or the proportion of patients who experience a particular side effect from a medication.
- Education:Partial relative frequency distributions can be used to describe the distribution of student grades, such as the proportion of students who receive a particular grade on a test or the proportion of students who pass a particular course.
- Business:Partial relative frequency distributions can be used to describe the distribution of sales, such as the proportion of sales that come from a particular product or the proportion of sales that are made to a particular customer.
Quick FAQs
What is the purpose of a partial relative frequency distribution?
A partial relative frequency distribution provides a concise summary of data, enabling researchers to understand the distribution of data points, identify patterns, and make comparisons between different sets.
How is a partial relative frequency distribution constructed?
A partial relative frequency distribution is constructed by dividing data into specific intervals and calculating the relative frequency within each interval, which is the number of data points in the interval divided by the total number of data points.
What are the applications of a partial relative frequency distribution?
Partial relative frequency distributions are used in various fields, including healthcare, education, and business, to describe data distribution, make comparisons, and identify trends and patterns.
What are the limitations of a partial relative frequency distribution?
Partial relative frequency distributions are sensitive to class interval size and can be biased due to subjective grouping, so it is important to choose appropriate class intervals and consider the potential for bias.


