Big ideas learning answers geometry embarks on an illuminating journey into the fascinating realm of geometry, where fundamental concepts, deductive reasoning, and practical applications converge to unravel the mysteries of shapes, angles, and spatial relationships.

From the basic building blocks of points, lines, and planes to the intricate world of three-dimensional shapes and coordinate geometry, this comprehensive guide provides a clear and engaging roadmap for mastering geometric principles.

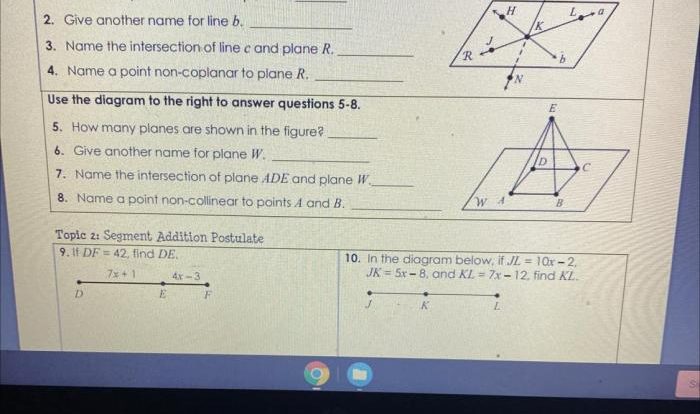
Geometry Fundamentals

Geometry, a branch of mathematics, delves into the study of shapes, their sizes, and their relationships. It forms the foundation for understanding the spatial world around us, from the structures we build to the objects we interact with daily.

At the core of geometry lie fundamental concepts like points, lines, planes, and angles. Points represent specific locations in space, while lines are collections of points extending infinitely in one direction. Planes are two-dimensional surfaces that extend infinitely in all directions, and angles are formed by the intersection of two lines or rays.

Geometric Shapes and Properties

Geometry encompasses a vast array of shapes, each with its unique properties. Basic shapes include triangles, squares, circles, and cubes. Triangles are three-sided polygons, characterized by their three angles and three sides. Squares are quadrilaterals with four equal sides and four right angles.

Circles are closed curves defined by a fixed distance from a central point. Cubes are three-dimensional shapes with six square faces.

These shapes possess specific properties that define their characteristics. For instance, the sum of the interior angles of a triangle is always 180 degrees, while the area of a circle is given by the formula πr², where r is the radius.

Geometric Transformations

Geometric transformations involve manipulating shapes by moving, rotating, or reflecting them. These transformations include translation, rotation, reflection, and dilation.

Translation involves moving a shape from one point to another without changing its size or orientation. Rotation involves turning a shape around a fixed point by a specific angle. Reflection involves flipping a shape over a line, creating a mirror image.

Dilation involves increasing or decreasing the size of a shape by a specific factor.

Geometric Reasoning

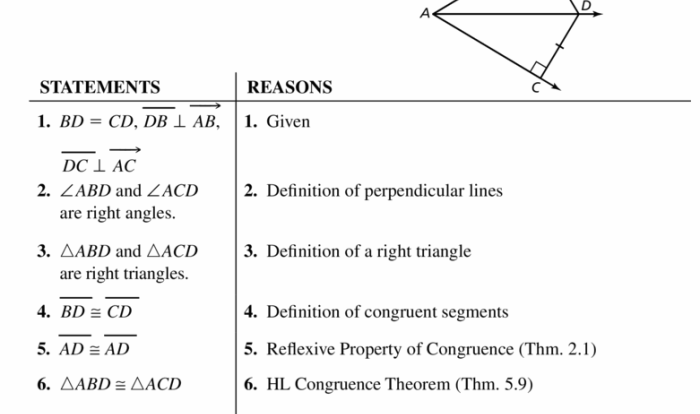
Geometric reasoning is the process of using logical arguments to solve geometry problems. It involves using deductive reasoning to derive new conclusions from known facts and principles.

In geometry, postulates, theorems, and corollaries play a crucial role in geometric proofs. Postulates are statements that are assumed to be true without proof. Theorems are statements that have been proven to be true based on the postulates. Corollaries are statements that follow directly from theorems.

Geometric Constructions

Geometric constructions are methods for creating geometric figures using only a compass and straightedge. These constructions are used to solve a variety of geometry problems, such as constructing perpendicular bisectors, angle bisectors, and parallel lines.

• Constructing a perpendicular bisector:To construct a perpendicular bisector of a line segment, follow these steps:
1. Draw a circle with center at one endpoint of the line segment and radius greater than half the length of the line segment.
2. Draw a circle with center at the other endpoint of the line segment and the same radius.
3. The two circles will intersect at two points. Draw a line through these two points. This line will be the perpendicular bisector of the line segment.
• Constructing an angle bisector:To construct an angle bisector, follow these steps:
1. Draw an arc that intersects both sides of the angle.
2. Draw another arc with the same radius that intersects the first arc and both sides of the angle.
3. Draw a line through the two points of intersection. This line will be the angle bisector.
• Constructing parallel lines:To construct parallel lines, follow these steps:
1. Draw a line segment.
2. Draw a line through one endpoint of the line segment that is perpendicular to the line segment.
3. Draw a line through the other endpoint of the line segment that is parallel to the first line.

Coordinate Geometry

Coordinate geometry is a branch of geometry that uses a coordinate system to represent points, lines, and shapes in a plane or space. It allows us to describe geometric objects using algebraic equations and perform geometric operations using algebraic techniques.

The coordinate plane is a two-dimensional plane with two perpendicular axes, the x-axis and the y-axis. Each point in the plane is represented by an ordered pair of numbers (x, y), where x is the distance from the point to the y-axis, and y is the distance from the point to the x-axis.

Plotting Points

To plot a point on the coordinate plane, we start at the origin (0, 0) and move x units along the x-axis and y units along the y-axis. For example, to plot the point (3, 4), we start at the origin and move 3 units to the right along the x-axis and 4 units up along the y-axis.

Drawing Graphs, Big ideas learning answers geometry

A graph is a visual representation of a set of data points. In coordinate geometry, we can use graphs to represent equations. To graph an equation, we plot the points that satisfy the equation and then connect the points with a smooth curve.

Equations of Lines

The equation of a line in coordinate geometry is typically written in the form y = mx + b, where m is the slope of the line and b is the y-intercept. The slope of a line is a measure of its steepness, and the y-intercept is the point where the line crosses the y-axis.

Equations of Circles

The equation of a circle in coordinate geometry is typically written in the form (x – h)^2 + (y – k)^2 = r^2, where (h, k) is the center of the circle and r is the radius.

Vectors and Matrices

Vectors and matrices are mathematical tools that can be used to represent and manipulate geometric objects in coordinate geometry. Vectors are used to represent directed line segments, and matrices are used to represent transformations of the coordinate plane.

Solid Geometry

Solid geometry delves into the properties and characteristics of three-dimensional shapes, exploring their unique attributes and relationships.

It encompasses the concepts of volume and surface area, providing a framework for understanding the spatial relationships and measurements of these shapes.

Furthermore, solid geometry introduces the concept of nets, which are two-dimensional representations of three-dimensional shapes, enabling us to visualize and construct these objects.

Properties and Characteristics of Three-Dimensional Shapes

Three-dimensional shapes, also known as solids, possess distinct properties and characteristics that define their form and behavior.

• Cubes:Regular hexahedrons with six square faces, eight vertices, and twelve edges. They exhibit high symmetry and stability.
• Spheres:Perfectly round shapes with no edges or vertices. They have a constant radius and exhibit rotational symmetry.
• Pyramids:Polyhedrons with a polygonal base and triangular faces that meet at a common vertex. They can be regular or irregular, depending on the symmetry of their base.

Volume and Surface Area

Volume and surface area are crucial concepts in solid geometry, providing quantitative measures of the space occupied and the external surface of three-dimensional shapes.

Volume represents the amount of three-dimensional space enclosed within a shape, while surface area measures the total area of its external surfaces.

Understanding volume and surface area is essential for various applications, such as calculating the capacity of containers, estimating the surface area of objects for painting or coating, and determining the mass of objects based on their density.

Nets

Nets are two-dimensional representations of three-dimensional shapes, serving as templates for constructing these objects.

They are formed by unfolding the faces of a three-dimensional shape into a flat plane, providing a visual aid for understanding the shape’s structure and assembly.

Nets are commonly used in packaging, origami, and architectural design, enabling the efficient creation of complex three-dimensional forms from two-dimensional materials.

Applications of Geometry

Geometry finds practical applications in diverse fields, from architecture and engineering to art and design. It plays a crucial role in shaping our world and solving real-world problems.

In architecture, geometric principles guide the design and construction of buildings, bridges, and other structures. Architects use geometry to create aesthetically pleasing and structurally sound designs, ensuring stability and functionality.

Engineering

In engineering, geometry is essential for designing and analyzing machines, vehicles, and other complex systems. Engineers apply geometric principles to optimize performance, efficiency, and safety.

• Civil engineers use geometry to design roads, bridges, and buildings, ensuring structural integrity and stability.
• Mechanical engineers use geometry to design engines, turbines, and other mechanical components, optimizing efficiency and performance.
• Aerospace engineers use geometry to design aircraft, spacecraft, and other vehicles, ensuring aerodynamic efficiency and flight stability.

Art

In art, geometry is used to create visually appealing and meaningful works. Artists use geometric shapes, patterns, and perspective to convey emotions, tell stories, and explore abstract concepts.

• Painters and sculptors use geometry to create compositions that are balanced, harmonious, and visually appealing.
• Architects and designers use geometry to create buildings and spaces that are both aesthetically pleasing and functional.
• Graphic designers use geometry to create logos, branding, and other visual elements that are both visually striking and effective.

Problem-Solving

Geometry also plays a significant role in problem-solving and critical thinking. By applying geometric principles, we can develop logical reasoning skills, spatial visualization abilities, and problem-solving strategies.

• Geometrical reasoning helps us to analyze and solve problems involving shape, size, and spatial relationships.
• Spatial visualization skills enable us to mentally manipulate and visualize objects in three-dimensional space.
• Problem-solving strategies based on geometry can be applied to a wide range of fields, from science and engineering to everyday life.

FAQ Guide: Big Ideas Learning Answers Geometry

What is the significance of postulates, theorems, and corollaries in geometry?

Postulates, theorems, and corollaries are the foundational building blocks of geometric proofs. Postulates are accepted as true without proof, theorems are statements that can be proven using postulates and other theorems, and corollaries are statements that follow directly from theorems.

How is coordinate geometry used in real-world applications?

Coordinate geometry is widely used in fields such as architecture, engineering, and computer graphics. It allows for the precise representation and manipulation of geometric shapes in two and three dimensions.

What are the key concepts to understand in solid geometry?

Solid geometry deals with three-dimensional shapes. Key concepts include volume, surface area, and the relationships between different types of solids, such as cubes, spheres, and pyramids.